CacheLab 报告
Published in GitHub, 2026
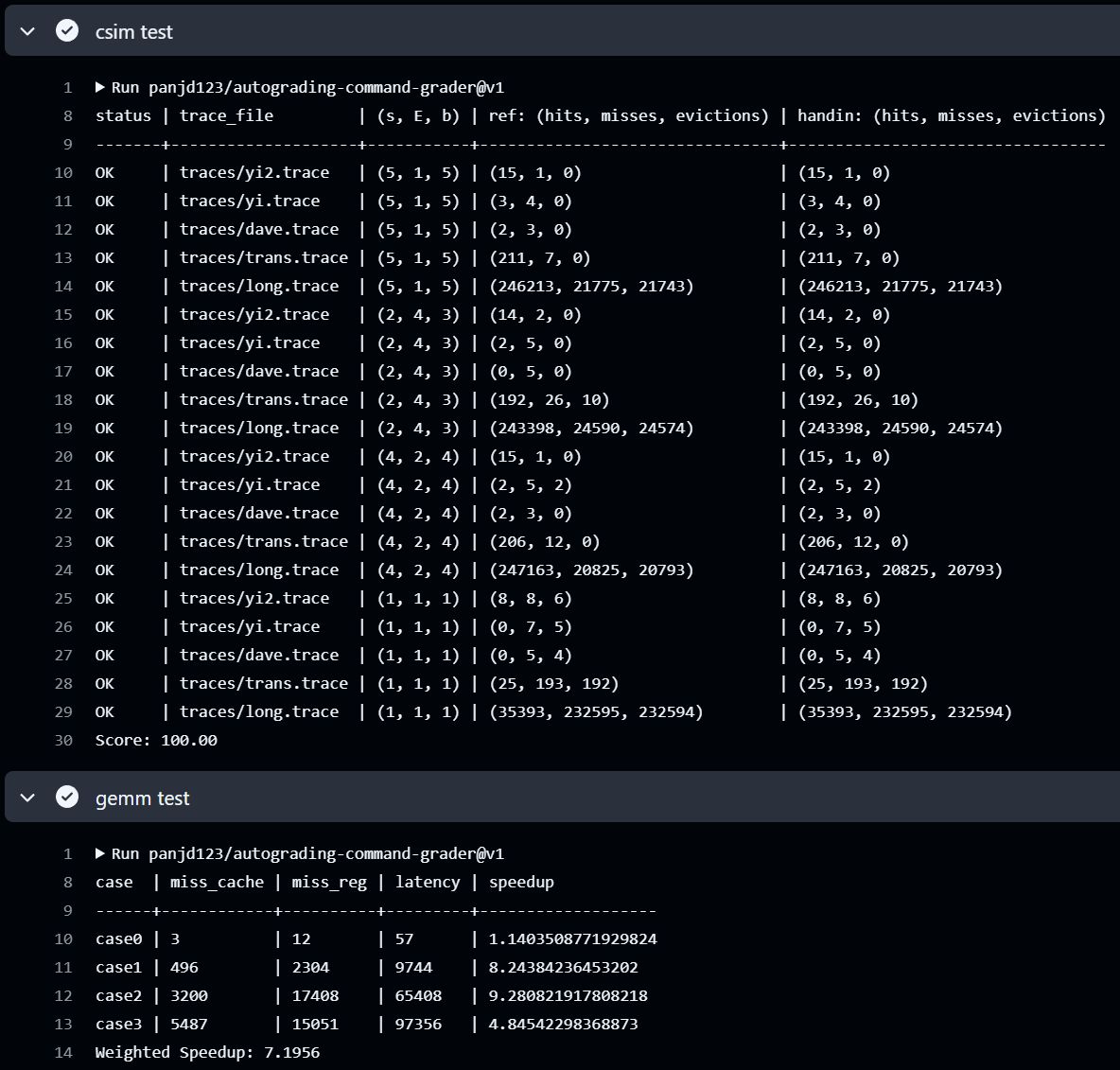
| csim 分数 | case1 speedup | case2 speedup | case3 speedup | weighted speedup |
|---|---|---|---|---|
| 100.00 | 8.24 | 9.28 | 4.85 | 7.20 |
Autograder 截图:
Part A: cache 模拟器
实现简述
缓存的核心数据结构由 class Line 表示,其中包含 valid 位、tag 和用于实现 LRU 策略的 last_used。
对于每一次内存访问,程序会根据地址计算对应的 set index 与 tag,随后搜索是否命中;若命中,则更新命中计数并设置行的时间戳。若未命中,则首先尝试填入空行;若没有空行,则依据 LRU 策略选出最久未使用的行进行替换,同时更新其 tag 与时间戳,并记录一次 eviction。对 modify(M) 指令,程序会执行两次访问,每次都更新命中计数与时间戳。
亮点
无
Part B: 矩阵乘法优化
亮点
- 矩阵分块
- 用寄存器预存矩阵数据,避免重复读取,从而减少
cache_miss和reg_miss case3矩阵二级分块
我认为的最优秀的实现排序
- case1
- case2
- case3
NOTE 每个
case上的多次调参以及较小的优化略过不表,只保留几次突破较大的优化。
case1
第一次优化
naive GEMM 的缺点主要有:跨行访问严重、寄存器重复加载频繁。因此,拿到这个 case 我们首先想到:要消除不连续的访问、通过分块放大局部性收益。
由于假设的硬件环境为 s = 5,E = 1,b = 4 ,所以一个 block 包含 16 bytes ,所以一个 line 恰好能存储 4 个 int 。所以只要让计算过程中每次访问的 A 或 B 的连续 4 个元素对齐到同一 block ,就能显著减少 miss 。在 \(16 \times 16\) 的矩阵中,我们尝试采用 \(4×4\) 分块,用分块后的小矩阵作为运算单元,运算后再归位并累加。这样分块使块内数据能正好落入一个 cache line 中,从而较好地利用空间局部性。
伪代码如下:
for k in 0..15 step 8:
for j in 0..15 step 8:
for i in 0..15 step 8:
for ii in i..i+7:
Load C[ii][j..j+7] into tempC[8]
Load A[ii][k..k+7] into tempA[8]
for kk in k..k+7:
Load B[kk][j..j+7] into tempB[8]
for t in 0..7:
tempC[t] += tempA[kk - k] * tempB[t]
Write tempC back to C[ii][j..j+7]
这个优化的加速比为 5.63 , miss_cache 为 661 , miss_reg 为 4352 。
第二次优化
在第一次优化中,我们似乎已经把矩阵分块方面做的很好了。所以我们想到,接下来可以尽可能增加寄存器的复用。很自然地想到 case0 的最终优化方法:把一个块内的数据全部读到寄存器内,然后暴力计算。但是如果要把块内数据全部读入寄存器,那么分块的大小就不能太大(因为我们只有36个寄存器可以用),但如果分块太小,又会增加cache miss。但是在第一次优化中我们采用的 \(4 \times 4\) 分块恰好可以将块内的数据全部读入寄存器(内层k循环外维护16个寄存器,k循环内对A和B各维护4个寄存器,共24个)。
伪代码如下:
for i in 0..15 step 4:
for j in 0..15 step 4:
init reg temp[4][4] = 0
for k in 0..15:
Read A[i..i+3][k] as a[4]
Read B[k][j..j+3] as b[4]
for p in 0..3:
for q in 0..3:
temp[p][q] += a[p] * b[q]
Write temp[4][4] to C[i..i+3][j..j+3]
这种优化下加速比达到了 8.2438 , miss cache 为 496 , miss reg 为 2304 。
下面我们分析一下这个结果:
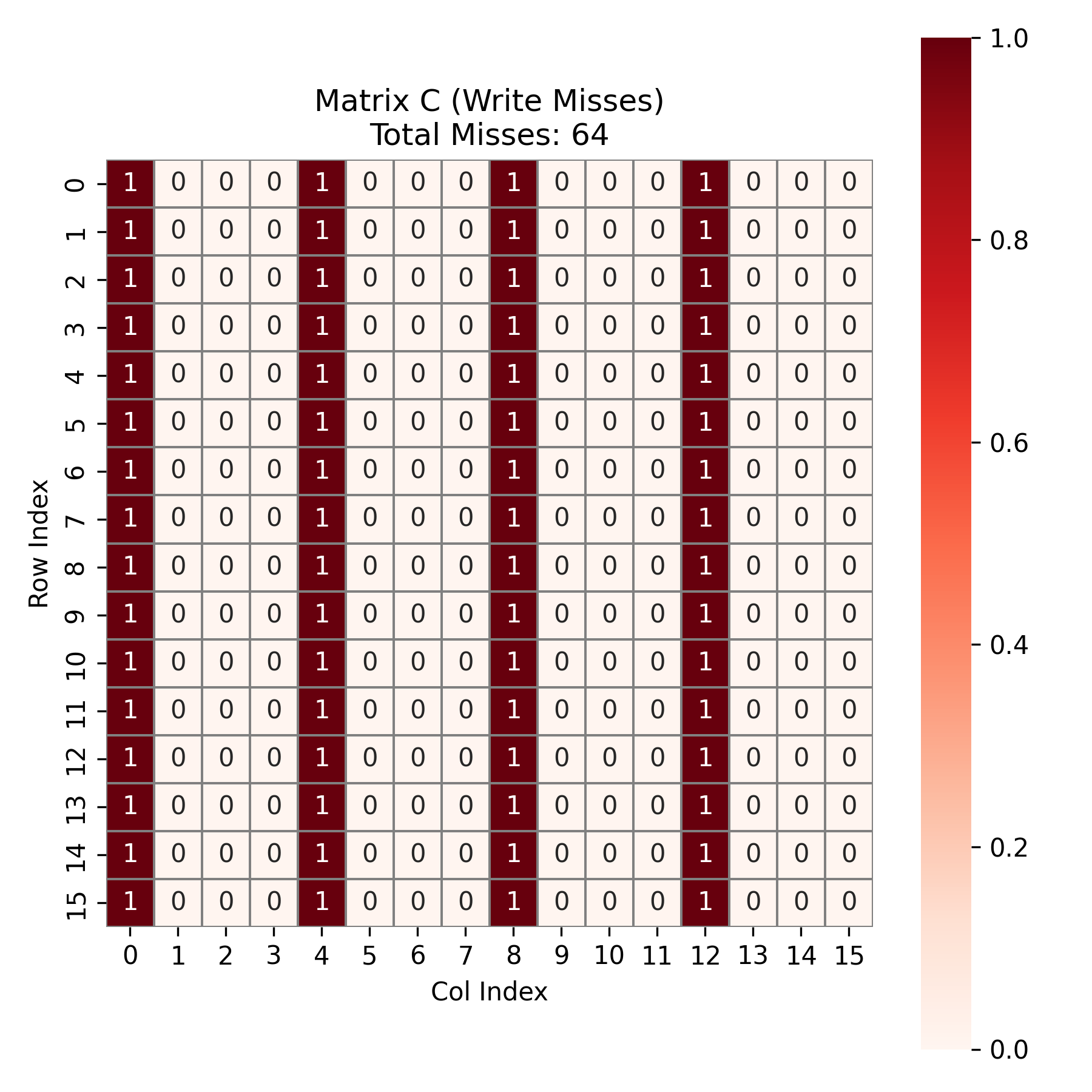
先分析矩阵 \(C\) 。在内层循环结束之后,程序会在每个 block_i , block_j 块的末尾,一次性连续写入 \(4 \times 4\) 的结果块。\(C\) 矩阵总共 \(16 \times 16 = 256\) 个元素。由于 \(b=4\),每写入 4 个元素填满一个 cache Line 并触发一次 miss 。故总共有 \(256 \div 4 = 64\) 次 miss 。如下图所示:
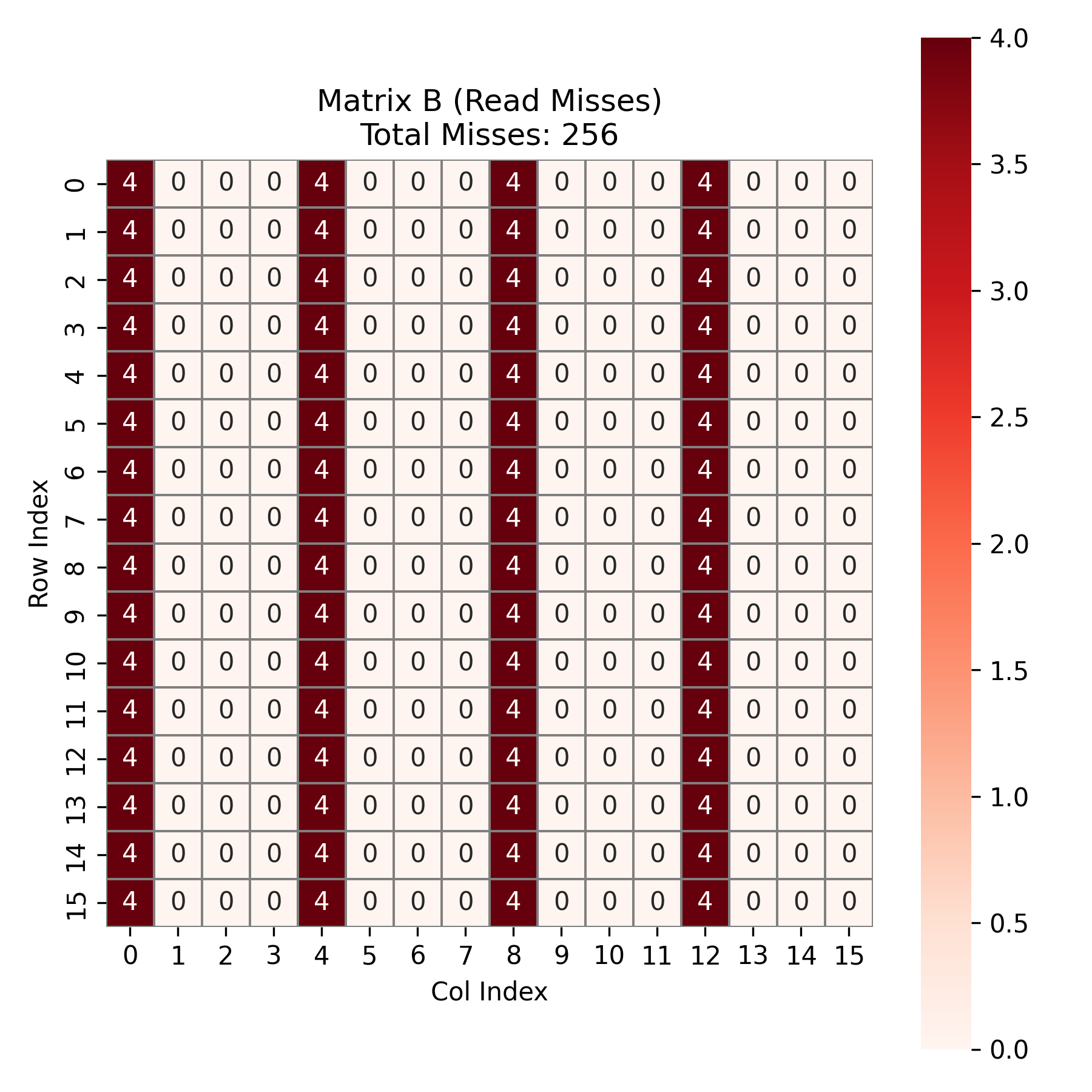
接下来是矩阵 \(B\)。在每个 block_i , block_j 的宏块内,k 从 0 循环到 15 ,这意味着我们遍历了 \(B\) 的全部 16 行。由于 cache 只能容纳 \(B\) 的一半,当读取 \(B\) 的第 8 行时,会驱逐第 0 行的数据。因此,\(B\) 矩阵完全没有时间局部性。所以,总共 16 个宏块,每个宏块内需要读取 \(B\) 的全部 16 行数据。总共发生 \(16 \times 16 = 256\) 次 miss。如图所示:
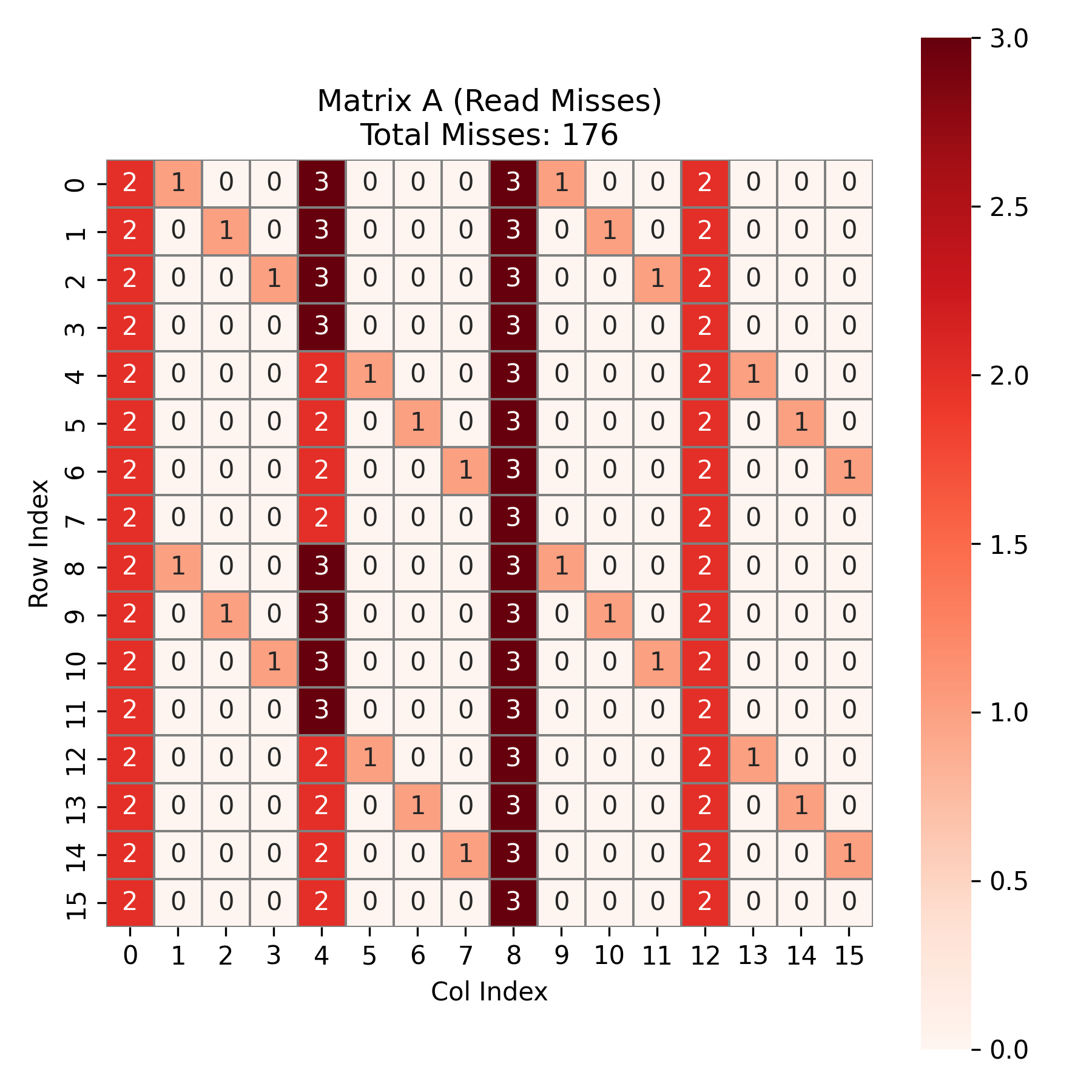
最后是最难分析的矩阵 \(A\) 。在理想情况下, \(A\) 在 block_j 循环中是不变的。只有第一列 (block_j=0)是冷不命中,后续三列(block_j=4,8,12)应该是 hit。
但实际上,\(A\) 和 \(B\) 会竞争有限的 cache sets 。由于 \(A\) 的读取方式是按列读取 4 行 (\(a_0...a_3\)),且 block_i 对齐,故 \(A\) 的数据总是固定落在 cache 的 set 0, 4, 8, 12 与镜像的 set 16, 20, 24, 28 上。而 \(B\) 的读取随着 k 变化,其 set 映射会扫过 cache 。但是,block_j 的不同偏移决定了 B 经过的起始 set 。
我们分析 \(4 \times 4\) 个宏块的分布:
第一列:这是每个
block_i的第一次读取,没有任何数据在cache中。固有 \(4 \times 16 = 64\) 次冷不命中。后三列:如果 \(B\) 与 \(A\) 产生了冲突 ,那么 \(A\) 就会被驱逐。在某些块中(例如
block_j=0及其对角线衍生位置),\(B\) 的读取覆盖了 \(A\) 所在的set 0, 4...,导致 \(A\) 被踢出。当下一个块需要 \(A\) 时,必须重新读取,于是产生了miss。在余下的12个本该复用的块中,有7个块被 \(B\) 驱逐,只有5个块实现了复用。固有 \(7\) 个冲突块 \(\times\) \(16\) 次读取 = \(112\) 次miss。A 的总cache miss为:\(64 + 112 = 176\) 次cache miss。如图所示:
综上,总共有 \(64 + 256 + 176 = 496\) 次 cache miss ,与测试结果相符合。
case2
[!NOTE]
case2的思路与case1是类似的,这个部分就不过多分析了
由 case1 的分析,\(4 \times 4\) 分块有良好的空间局部性,并且在参考附录中几篇文章的策略后, case2 中仍然采用 \(4 \times 4\) 分块。
这个优化的加速比为 9.28 ,miss_cache 为 3200 ,miss_reg 为 17408 。
下面简单分析一下cache_miss。
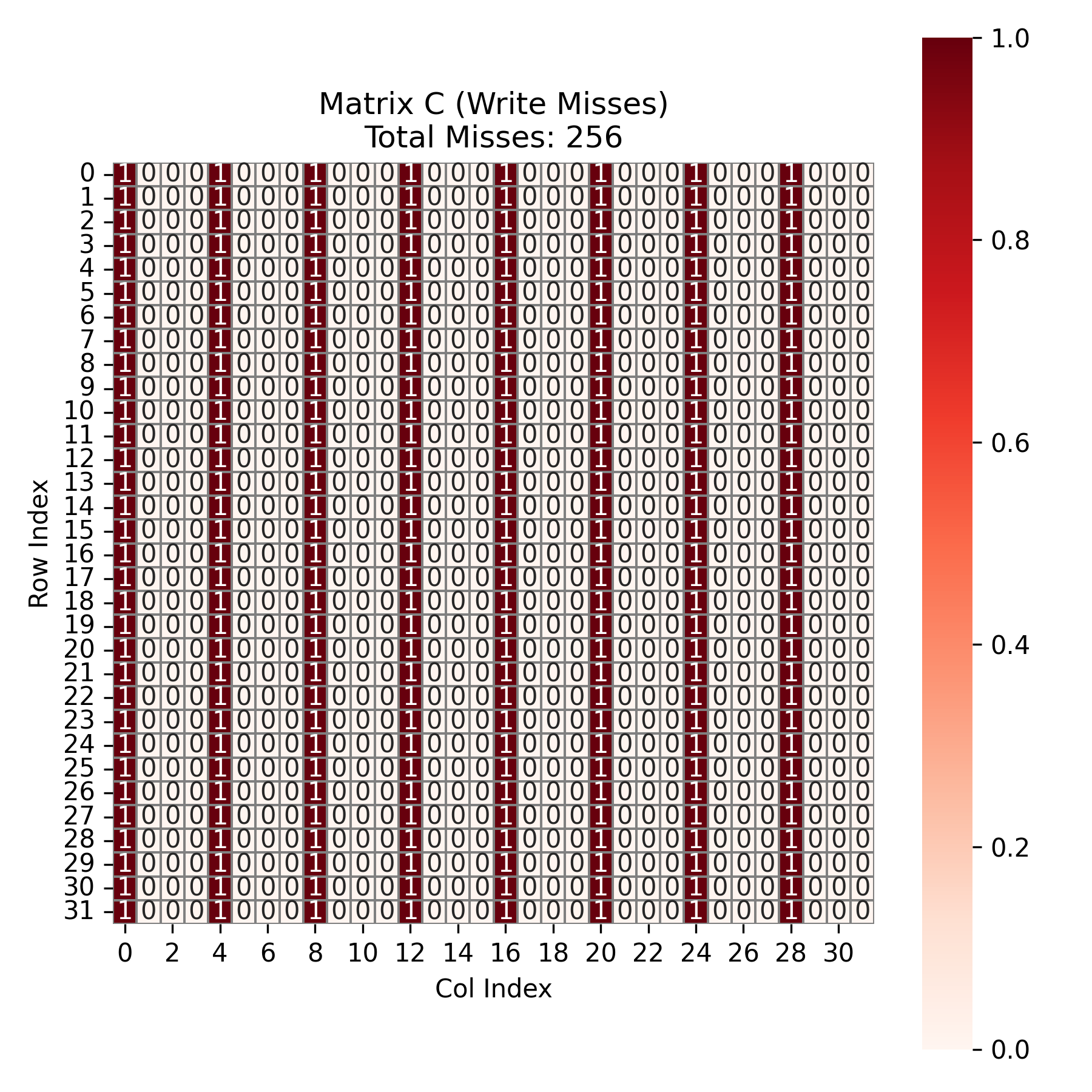
对于矩阵 \(C\) ,由于 \(C\) 的大小为 \(32 \times 32 = 1024\) ,故 miss 次数为 \(1024 \div 4 = 256\) 次。如图所示:
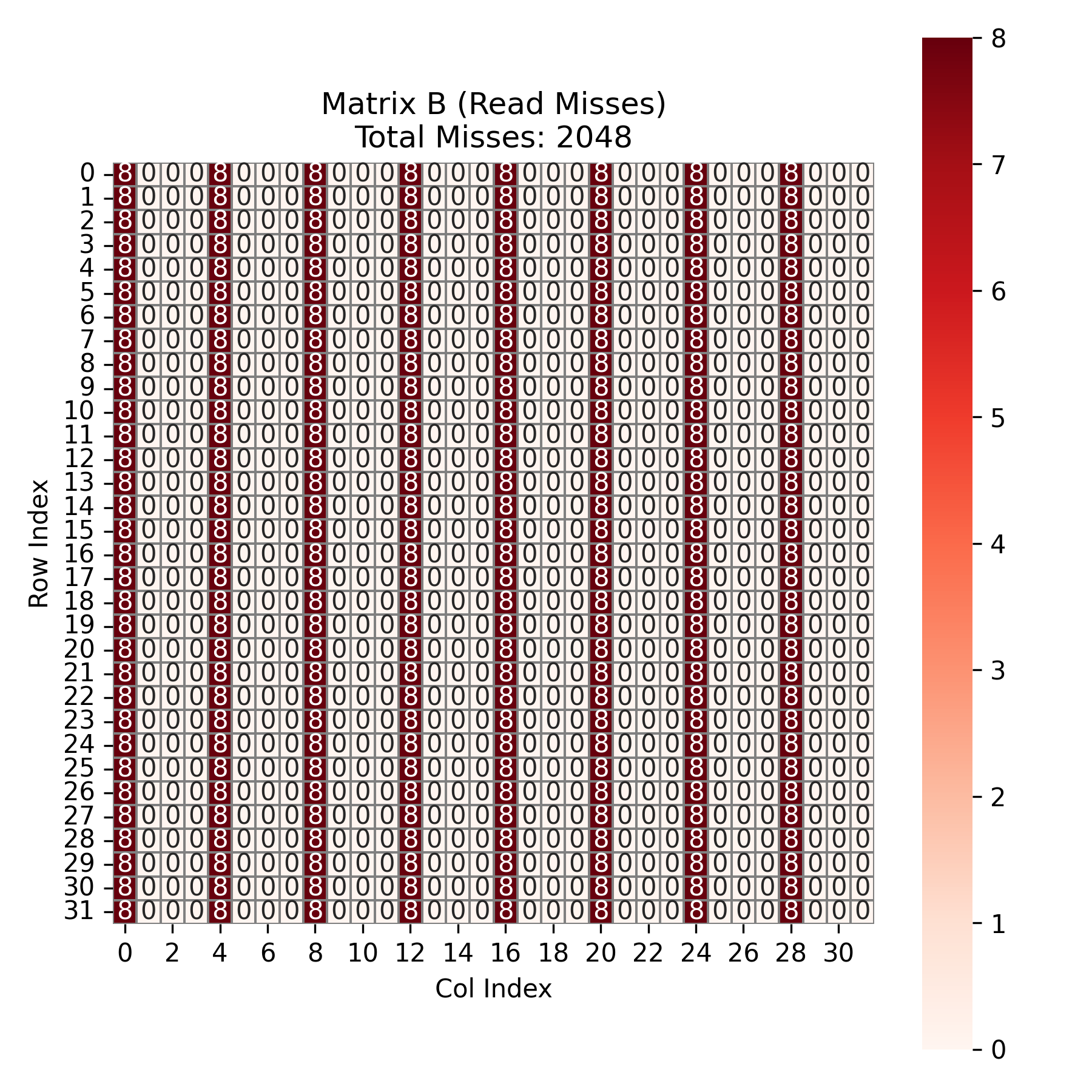
对于矩阵 \(B\) ,在每个k循环,由于4个int刚好装满一个 cache block ,故除第一次访问 miss ,之后 3 次为 hit 。故 k 循环走完会产生 32 次 miss 。而总共有8个 block_i 与 8 个 block_j ,故一共产生 \(32 \times 8 \times 8 = 2048\) 次 miss 。如图所示:
对于矩阵 \(A\),与 case1 中的情况是一样的,因 \(A\) 与 \(B\) 的冲突而产生 miss 。如图,总共有 896 次 miss 。
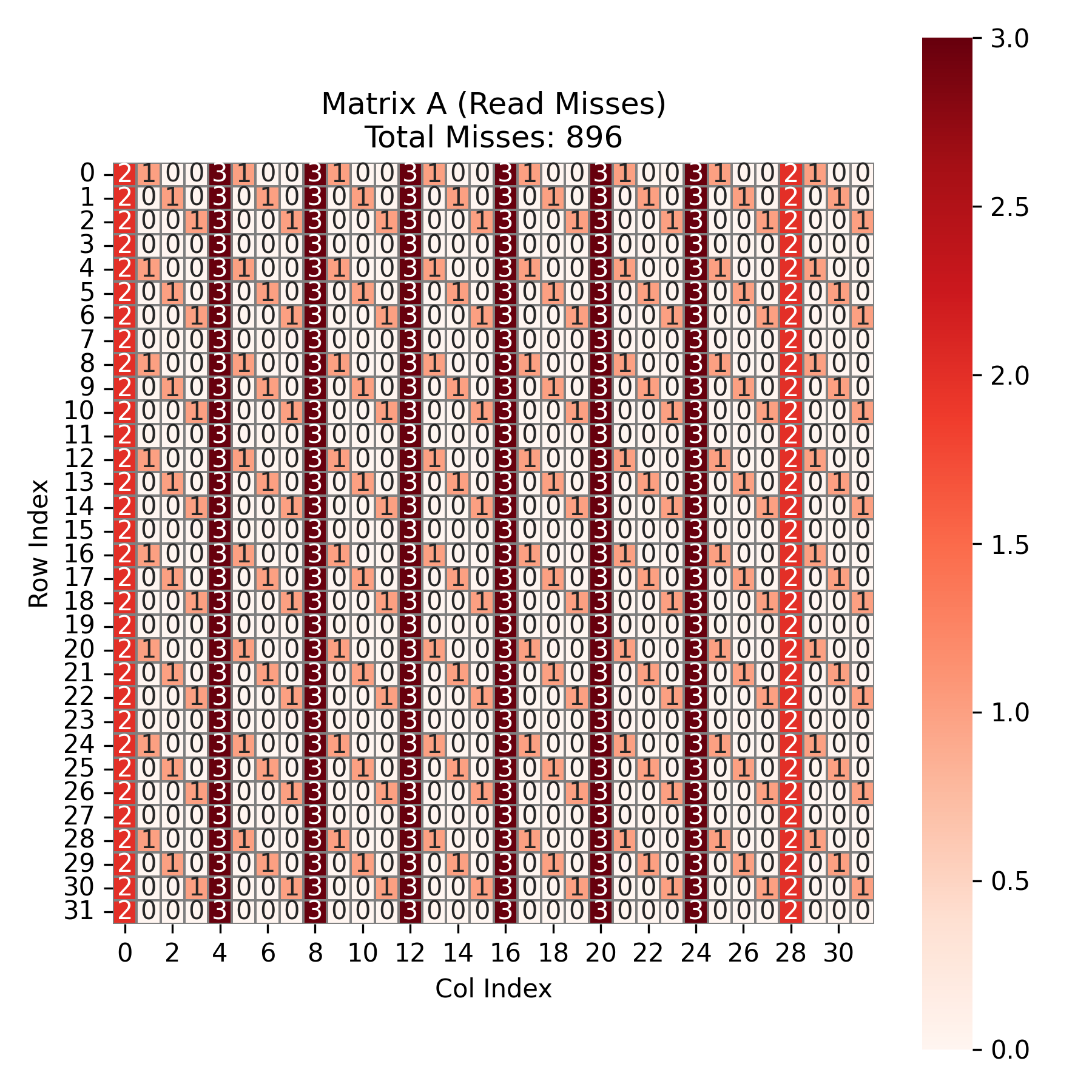
综上,总共与 \(256 + 2048 + 896 = 3200\) 次 miss 。与测试结果相符合。
case3
在一位师兄的建议与一篇博客的启发下,这个 case 我选择的策略是:对矩阵中可以分块的子矩阵分块,然后对边界剩余部分分别处理。
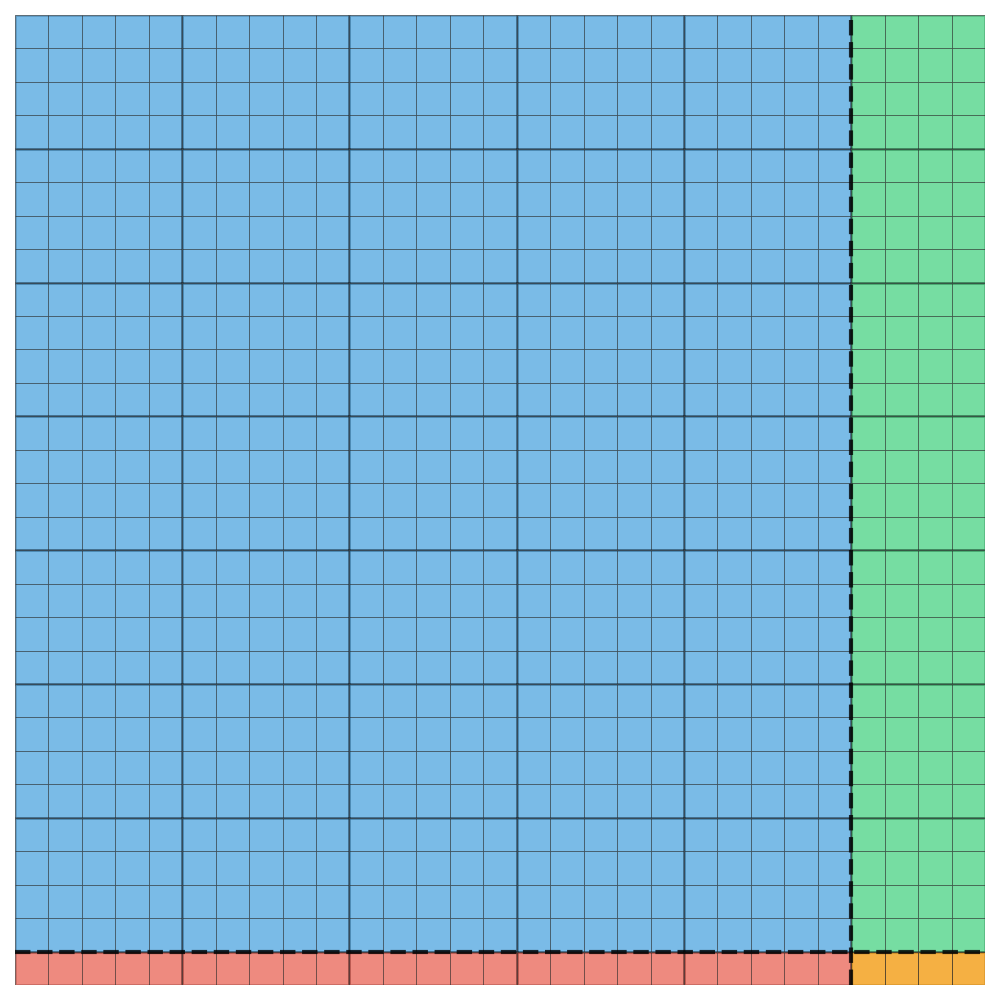
我们选择 \(4 \times 5\) 作为输出矩阵 \(C\) 的主分块大小。矩阵 \(C\) 被划分为四个区域:
主体块区域:\(28 \times 25\) (行 0~27,列 0~24),使用 \(4 \times 5\) 分块完全覆盖。
右侧剩余列区域:\(28 \times 4\) (行 0~27,列 25~28),使用 \(4 \times 4\) 分块处理。
底部剩余行区域:\(1 \times 25\) (行 28,列 0~24),使用 \(1 \times 5\) 分块处理。
右下角小块区域:\(1 \times 4\) (行 28,列 25~28)。
如图:
这个 case 的伪代码如下:
for block_i in 0..M-3 step 4:
for block_j in 0..N-4 step 5:
init reg c[4][5] = 0
for k in 0..K-1:
Read A[block_i..block_i+3][k] as a[4]
Read B[k][block_j..block_j+4] as b[5]
for p in 0..3:
for q in 0..4:
c[p][q] += a[p] * b[q]
Write c[4][5] to C[block_i..block_i+3][block_j..block_j+4]
for block_i in 0..M-3 step 4:
init reg c[4][4] = 0
for k in 0..K-1:
Read A[block_i..block_i+3][k] as a[4]
Read B[k][25..28] as b[4]
for p in 0..3:
for q in 0..3:
c[p][q] += a[p] * b[q]
Write c[4][4] to C[block_i..block_i+3][25..28]
for block_j in 0..N-4 step 5:
init reg c[1][5] = 0
for k in 0..K-1:
Read A[28][k] as a[1]
Read B[k][block_j..block_j+4] as b[5]
for p in 0..0:
for q in 0..4:
c[p][q] += a[p] * b[q]
Write c[1][5] to C[28][block_j..block_j+4]
init reg c[1][4] = 0
for k in 0..K-1:
Read A[28][k] as a[1]
Read B[k][25..28] as b[4]
for p in 0..0:
for q in 0..3:
c[p][q] += a[p] * b[q]
Write c[1][4] to C[28][25..28]
加速比为 4.85 , miss_cache 为 5487 , miss_reg 为 15051 。
下面我们简单分析一下 cache_miss 。
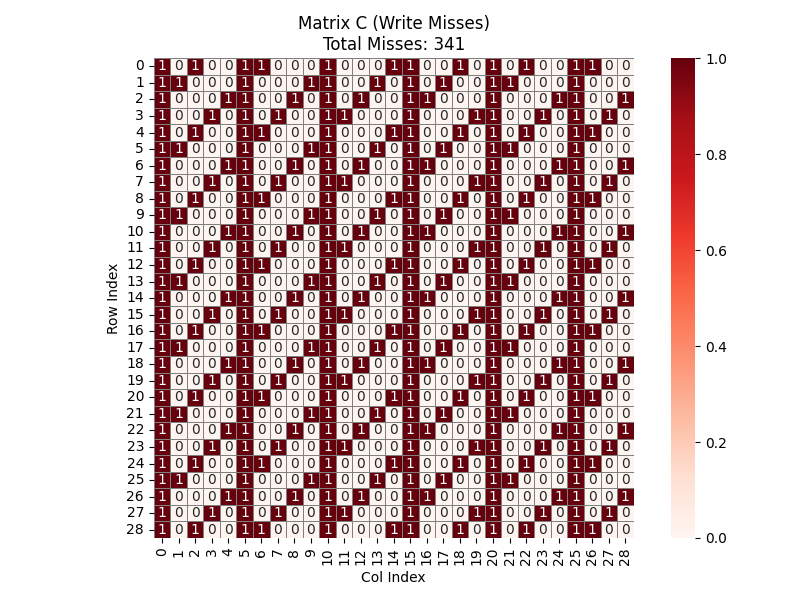
先分析矩阵 \(C\) 。我们知道一个 cache line 可以存储 4 个 int ,而矩阵行、列并非 4 的倍数,所以 \(C\) 的首地址并不是在一个 cache line 的 0 号位。计算后知道 \(C\) 的首地址应该在 line 的 3 号位。同时,由于 \(N=29\),每一行的起始地址相对于 cache line 的偏移量都会发生变化。由 \(29 \mod 4 = 1\) ,我们知道每一行的起始位置都会比上一行右移一格。主循环中一次写入 5 个元素,占据 20 bytes。所以无论起始位置在哪,写入五个元素必然会跨越两个 cache line 。这意味着处理每一个 block 时,写入 \(C\) 的一行往往需要触发 2 次 miss,而不是理想情况下的 1 次。如图, \(C\) 的 cache_miss 为 341 次。
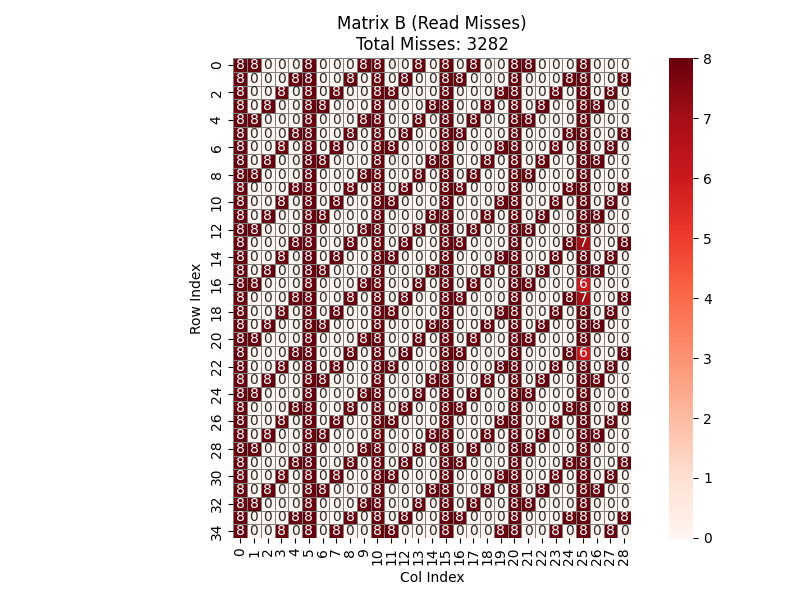
接下来是矩阵 \(B\)。外层循环 BI 步长为 4,处理矩阵需迭代 7 轮主循环(加上边缘处理共计约 8 轮扫描)。同时,每一轮扫描都会将前一轮的数据彻底替换。读取分块中的 5 个连续元素时,第一个元素占据了当前 line 的末尾,导致后续 4 个元素必须从下一个 line 中获取。由于 \(B\) 是按列块扫描,地址跳跃大,cache 无法同时驻留两个 line,导致原本 1 次加载能完成的任务变成了 2 次 miss。如图,最终的 miss 为 3282 次。
\(A\) 的 cache miss 分析难度很大,但可以知道 \(A\) 的绝大部分行块在每一轮循环中都因为 \(B\) 矩阵数据的涌入而被驱逐。也就是说,每一行每一轮都存在大量的冲突。具体的miss如下图所示。 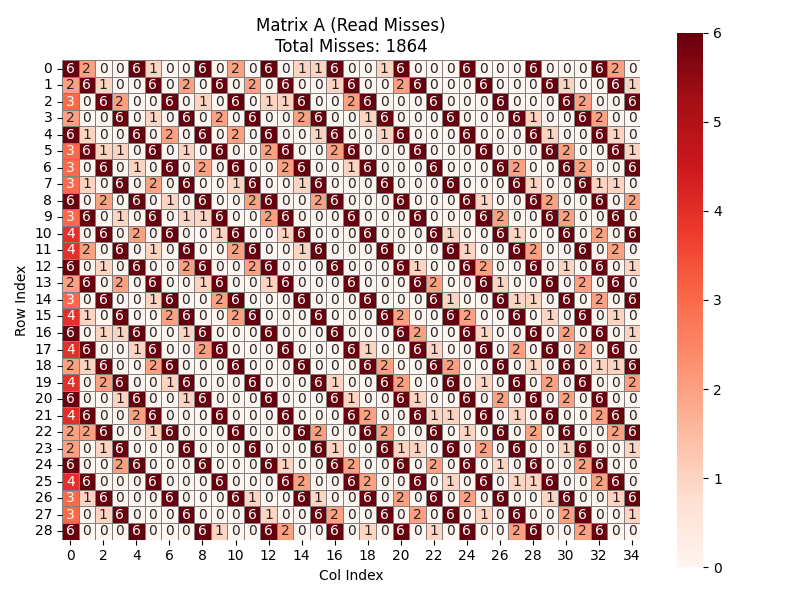
综上,总共有 \(341 + 3282 + 1864 = 5487\) 次 cache miss ,与测试结果相符合。
反馈/收获/感悟/总结
这个 lab 是我耗时最久、找资料时间最多、写的最难受的一个 lab。(也是求助大佬最多的一个lab) 在对网上资料的阅读中,在对大佬与前辈思路的研究中,我也确实学到了很多知识,收获了很多成就感。
case3的优化与分析简直痛苦无比。特别感谢 Gemini ,她简直是神。我在 case3 上花的时间最多,但最后也没有取得特别好的效果。最后一个星期本想好好研究一下case3,再尝试一些优化策略,但由于实在太忙,最后也没有继续优化,这部分的报告也写得比较潦草。有心无力,也是一种遗憾吧。
同时也有一点想吐槽的地方,就是感觉 Part 2 的打榜最后往往变成大家疯狂调超参数,为了 0.01 的加速比进步而绞尽脑汁。我的感觉是,不如设置一个满分线,达到一定加速比这个Part就算满分。当然这仅仅是我个人的观点。
总之这是一个体验超级棒的 lab 。感谢助教师兄师姐的付出!
参考的重要资料
北大学长的
cachelab指南,写的很详细,对一些坑点和难点解析很清楚,对我的Part A解决帮助很大
感谢这篇博客,为我的
Part B case3提供了很好的思路,“凑分块”的想法由此而来,这篇博客对我的Part B优化帮助很大
很棒的解析,让我对各种优化策略有了更深的理解。我最开始做
Part B就是从这里入门的
